Reference/API

Operations on Spectroscopic Data

speclite.accumulate Module

Stack spectra on the same wavelength grid using weighted accumulation.

Functions

accumulate(data1_in, data2_in[, data_out, ...])

Combine the data from two spectra.

speclite.downsample Module

Downsample spectra by combining adjacent pixels.

Functions

downsample(data_in, downsampling[, weight, ...])

Downsample spectral data by a constant factor.

speclite.resample Module

Resample spectra using interpolation.

Functions

resample(data_in, x_in, x_out, y[, ...])

Resample the data of one spectrum using interpolation.

speclite.redshift Module

Apply redshift transformations to wavelength, flux, inverse variance, etc.

Functions

redshift(z_in, z_out[, data_in, data_out, rules])

Transform spectral data from redshift z_in to z_out.

Operations with Filters

speclite.filters Module

Support for calculations involving filter response curves.

Overview

See Filter Response Curves for information about the standard filters included with this code distribution and instructions for adding your own filters. Filter names have two components, a group name and a band name, which are combined with a hyphen, e.g. “sdss2010-r”. The group names included with this package are:

>>> filter_group_names
['sdss2010', 'sdss2010noatm', 'decam2014', 'wise2010', 'hsc2017', 'lsst2016', 'bessell', 'BASS', 'MzLS', 'Euclid', 'decamDR1', 'decamDR1noatm', 'gaiadr2']

List the band names associated with any group using, for example:

>>> load_filters('sdss2010-*').names
['sdss2010-u', 'sdss2010-g', 'sdss2010-r', 'sdss2010-i', 'sdss2010-z']

Here is a brief example of calculating SDSS r,i and Bessell V magnitudes for a numpy array of fluxes for 100 spectra covering 4000-10,000 A with 1A pixels:

>>> import astropy.units as u
>>> wlen = np.arange(4000, 10000) * u.Angstrom
>>> flux = np.ones((100, len(wlen))) * u.erg / (u.cm**2 * u.s * u.Angstrom)

Units are recommended but not required (otherwise, the units shown here are assumed as defaults). Next, load the filter responses:

>>> import speclite.filters
>>> filters = speclite.filters.load_filters(
...     'sdss2010-r', 'sdss2010-i', 'bessell-V')

Finally, calculate the magnitudes to obtain an astropy Table of results with one row per input spectrum and one column per filter:

>>> mags = filters.get_ab_magnitudes(flux, wlen)

If you prefer to work with a numpy structured array, you can convert the returned table:

>>> mags = filters.get_ab_magnitudes(flux, wlen).as_array()

Padding

Under certain circumstances, you may need to pad an input spectrum to cover the full wavelength range of the filters you are using. See FilterResponse.pad_spectrum() and FilterSequence.pad_spectrum() for details on how this is implemented.

Shifted Filters

It can be useful to work with a filter whose wavelengths have been shifted, e.g. for the applications in http://arxiv.org/abs/astro-ph/0205243. This is supported with the FilterResponse.create_shifted() method, for example:

>>> wlen = np.arange(4000, 10000) * u.Angstrom
>>> flux = np.ones(len(wlen)) * u.erg / (u.cm**2 * u.s * u.Angstrom)
>>> r0 = speclite.filters.load_filter('sdss2010-r')
>>> rz = r0.create_shifted(band_shift=0.2)
>>> print(np.round(r0.get_ab_magnitude(flux, wlen), 3))
-21.359
>>> print(np.round(rz.get_ab_magnitude(flux, wlen), 3))
-20.963

Note that a shifted filter has a different wavelength coverage, so may require padding of your input spectra.

Convolutions

The filter response convolution operator implemented here is defined as:

\[F[R,f_\lambda] \equiv \int_0^\infty \frac{dg}{d\lambda}(\lambda) R(\lambda) \omega(\lambda) d\lambda\]

where \(R(\lambda)\) is a filter response function, represented by a FilterResponse object, and \(f_\lambda \equiv dg/d\lambda\) is an arbitrary differential function of wavelength, which can either be represented as a callable python object or else with arrays of wavelengths and function values.

The default weights:

\[\omega(\lambda) = \frac{\lambda}{h c}\]

are appropriate for photon-counting detectors such as CCDs, and enabled by the default setting photon_weighted = True in the methods below. Otherwise, the convolution is unweighted, \(\omega(\lambda) = 1\), but arbitrary alternative weights can always be included in the definition of \(f_\lambda\). For example, a differential function of frequency \(dg/d\nu\) can be reweighted using:

\[f_\lambda(\lambda) = \frac{dg}{d\lambda}(\lambda) = \frac{c}{\lambda^2} \frac{dg}{d\nu}(\nu = c/\lambda)\]

These definitions make no assumptions about the units of \(f_\lambda\), but magnitude calculations are an important special case where the units of \(f_\lambda\) must have the dimensions \(M / (L T^3)\), for example, \(\text{erg}/(\text{cm}^2\,\text{s}\,\AA)\).

The magnitude of \(f_\lambda\) in the filter band with response \(R\) is then:

\[m[R,f_\lambda] \equiv -2.5 \log_{10}(F[R,f_\lambda] / F[R,f_{\lambda,0}])\]

where \(f_{\lambda,0}(\lambda)\) is the reference flux density that defines the photometric system’s zeropoint \(F[R,f_{\lambda,0}]\). The zeropoint has dimensions \(1 / (L^2 T)\) and gives the rate of incident photons per unit telescope area from a zero magnitude source.

A spectral flux density per unit frequency, \(f_\nu = dg/d\nu\), should be converted using:

\[f_\lambda(\lambda) = \frac{c}{\lambda^2} f_\nu(\nu = c/\lambda)\]

for use with the methods implemented here.

For the AB system,

\[f_{\lambda,0}^{AB}(\lambda) = \frac{c}{\lambda^2} (3631 \text{Jy}) \; ,\]

and the convolutions use photon-counting weights.

Sampling

Filter responses are tabulated on non-uniform grids with sufficient sampling that linear interpolation is sufficient for most applications. When a filter response is convolved with tabulated data, we must also consider the sampling of the tabulated function. In this implementation, we assume that the tabulated function is also sufficiently sampled to allow linear interpolation.

The next issue is how to sample the product of a filter response and tabulated function when performing a numerical convolution integral. With the assumptions above, a safe strategy would be to sample the integrand at the union of the two wavelength grids. However, this is relatively expensive since it requires interpolating both the response and the input function. Interpolation is sometimes unavoidable: for example, when the function is linear and represented by its values at only two wavelengths.

The approach adopted here is to use the sampling grid of the input function to sample the convolution integrand whenever it samples the filter response sufficiently. This requires that the filter response be interpolated, but this operation only needs to be performed once when many convolutions are performed on the same input wavelength grid. Our criteria for sufficient filter sampling is that at most one filter wavelength point lies between any consecutive pair of input wavelength points. When this condition is not met, the input function will be interpolated at the minimum number of response wavelengths necessary to satisfy the condition.

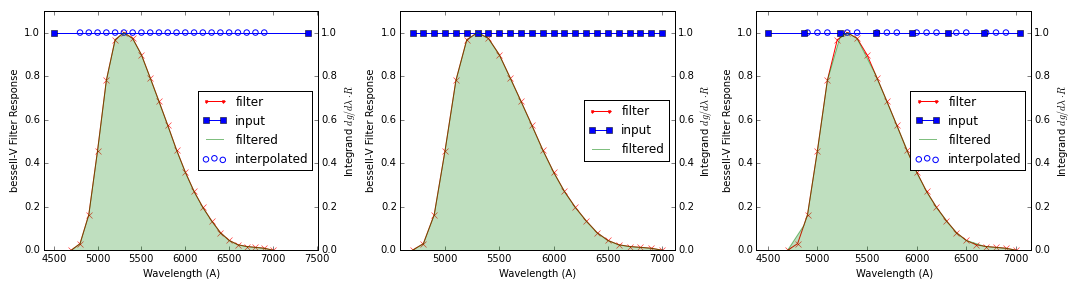
The figure below (generated by this function) illustrates three different sampling regimes that can occur in a convolution with the Bessell V filter (red curve). Filled blue squares show where the input function is sampled and open blue circles show where interpolation of the input function is performed. The left-hand plot shows an extremely undersampled input that is interpolated at every filter point. The middle plot shows a well sampled input that requires no interpolation. The right-hand plot shows an input that is slightly undersampled and requires interpolation at some of the filter points. All three methods give consistent results, with discrepancies of < 0.05%.

sampling explanatory plot

The logic described here is encapsulated in the FilterConvolution class. Interpolation is performed automatically, as necessary, by the high-level magnitude calculating methods, but FilterConvolution is available when more control of this process is needed to improve performance.

Performance

If the performance of magnitude calculations is a bottleneck, you can speed up the code significantly by taking advantage of the fact that all of the convolution functions can operate on multidimensional arrays. For example, calling FilterResponse.get_ab_magnitudes() once with an array of 5000 spectra is about 10x faster than calling it 5000 times with the individual spectra. However, in order to take advantage of this speedup, your spectra need to all use the same wavelength grid.

Note that the eliminating flux units (which are always optional) from your input spectra will only result in about a 10% speedup, so units are generally recommended.

Attributes

filter_group_nameslist

List of filter group names included with this package.

default_wavelength_unitastropy.units.Unit

The default wavelength units assumed when units are not specified. The same units are used to store wavelength values in internal arrays.

default_flux_unitastropy.units.Unit

The default units for spectral flux density per unit wavelength.

Functions

ab_reference_flux(wavelength[, magnitude])

Calculate an AB reference spectrum with the specified magnitude.

filter_sampling_explanatory_plot([save])

Generate an explanatory plot for the documentation.

load_filter(name[, load_from_cache, verbose])

Load a single filter response by name.

load_filters(*names)

Load a sequence of filters by name.

plot_filters(responses[, wavelength_unit, ...])

Plot one or more filter response curves.

tabulate_function_of_wavelength(function, ...)

Evaluate a function of wavelength.

validate_wavelength_array(wavelength[, ...])

Validate a wavelength array for filter operations.

Classes

FilterConvolution(response, wavelength[, ...])

Convolve a filter response with a tabulated function.

FilterResponse(wavelength, response, meta[, ...])

A filter response curve tabulated in wavelength.

FilterSequence(responses)

Immutable sequence of filter responses.

Other Functions

speclite.benchmark Module

Driver routines for benchmarking and profiling.

Functions

magnitude_calculation(results, num_repeats)

Run a suite of magnitude calclulations.

main([argv])

speclite.utils Package

Functions

get_path_of_data_file(data_file)

convenience wrapper to return location of data file